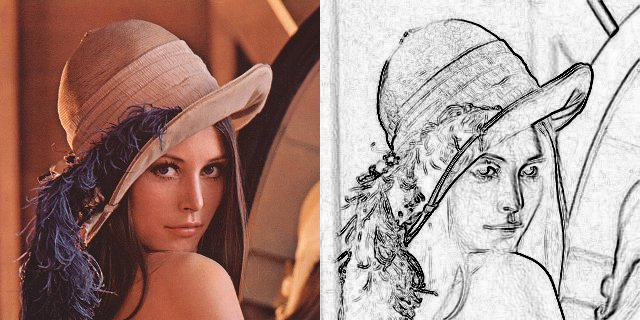
L’image numérique étant en quelque sorte une carte de pixels, on peut identifier chaque pixel par ses coordonnées X et Y et lui affecter une valeur liée à sa luminosité. On peut utiliser dans le cadre des images numériques une sorte de tableau de X colonnes et Y lignes qui réserve une place pour ranger la valeur de chaque pixel de l’image. En mathématique ce genre de tableau s’appelle une matrice, et les mathématiciens disposent d’outils pour effectuer des calculs sur les matrices, comme additionner deux matrices, les multiplier, etc …
La plupart des filtres de traitement d’images utilisent des matrices de convolution. Mais qu’est-ce que c’est qu’une matrice de convolution? Nous sommes là dans le coin des mathématiciens. On peut s’en faire une idée approximative sans utiliser les outils mathématiques que bien peu connaissent. Un produit de convolution est un traitement d’une matrice par une autre appelée matrice de convolution ou « noyau » (kernel).
Dans le cas qui nous intéresse, nous mettons en jeu deux matrices très différentes: la matrice image initiale input, très grande (par exemple 512 x 512) et une matrice plus petite (3×3 ou 5×5) qu’on appelle le noyau ou kernel parce que c’est le « coeur » de tous les changements qui vont affecter l’image.
Appliquer un filtre de convolution consiste à multiplier chacun des pixels de la matrice input par le noyau ou kernel. Pour calculer la valeur finale d’un pixel O(x, y) de la matrice image output, on multiplie sa valeur initiale I(x,y) par celle du pixel central du noyau et on additionne ensuite la valeur des produits des pixels adjacents.
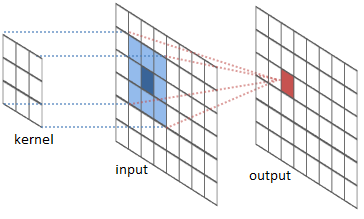
Pour calculer la valeur du pixel (x,y) de l’image output (en rouge) on superpose le centre du kernel (ici une matrice 3×3) sur le pixel source en position (x,y) (en bleu foncé) et on multiplie deux à deux les valeurs du kernel et de la zone couverte en bleue entre elles puis on les additionnent pour trouver la valeur de la sortie.
La valeur du pixel sera donnée, dans le cas d’un noyau 3×3, par la formule :
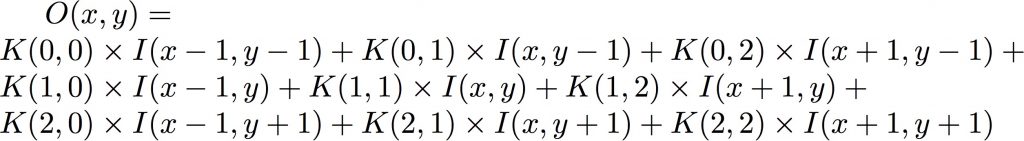
que l’on peut aussi écrire :
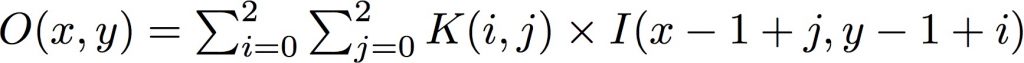
Il reste ensuite à diviser le résultat par le nombre d’éléments du noyau, cette dernière opération n’appartient pas au produit de convolution proprement dit, mais elle est nécessaire pour maintenir la dynamique de l’image ainsi que sa linéarité.
Cette formule est à appliquer sur les trois canaux RVB.
Il faut ensuite réitérer ces opérations sur tous les pixels en les adaptant pour ceux du bord.
Un exemple :
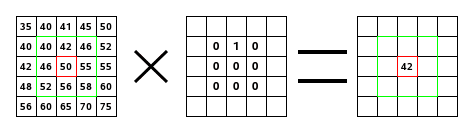
À gauche se trouve la matrice de l’image : chaque pixel est indiqué par sa valeur. Le pixel initial est encadré de rouge. La zone d’action du noyau est encadrée de vert. Au centre, se trouve le noyau et, à droite, le résultat de la convolution sur le pixel initial.
Voici ce qui s’est passé: le filtre a lu successivement, de gauche à droite et de haut en bas, les pixels de la zone d’action du noyau et il a multiplié chacun d’eux par la valeur correspondante du noyau et additionné les résultats. Le pixel initial a pris la valeur 42 : (40×0)+(42×1)+(46×0)+(46×0)+(50×0)+(55×0)+(52×0)+(56×0)+(58×0)=42 (le filtre dépose ses résultats sur une copie de l’image et pas directement dans l’image). Le résultat graphique est un décalage du pixel initial d’un pixel vers le bas.
La création de noyaux nécessite des connaissances mathématiques de haut niveau. Mais vous en trouverez de tout faits sur la Toile. En voici quelques exemples :
| Augmenter le contraste | Flou | Amélioration des bords |
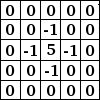 |  | 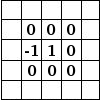 |
| Détection des bords | Repoussage | Filtre de Sobel |
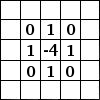 | 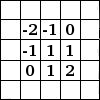 | 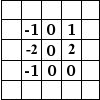 |
Exercice 1 : Avec le logiciel GIMP, ouvrir le fichier rose.jpg de l’activité précédente et testez les filtres ci-dessus dans le menu Filtre > Générique > Matrice de convolution.
Exercice 2 : Proposer un noyau qui décale l’image d’un pixel vers la droite
Exercice 3 : Commenter la fonction produit_convo du script suivant et testez-le avec différents noyaux
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 |
#-*- coding:Latin-1 -*- # PIL (Python Imaging Library) est une bibliothèque pour la manipulation des images from PIL import Image #============================================================ def produit_convo(Pix,Ker,Largeur,Hauteur): newPix=[] for p in range(Largeur*Hauteur): s=0 for i in range(5): if p-2*Largeur>=0: if abs((p-2*Largeur-2+i)%Largeur-(p-2*Largeur)%Largeur)<=2 : s=s+Ker[i]*Pix[p-2*Largeur-2+i] else: continue else: break for i in range(5): if p-Largeur>=0: if abs((p-Largeur-2+i)%Largeur-(p-Largeur)%Largeur)<=2 : s=s+Ker[5+i]*Pix[p-Largeur-2+i] else: continue else: break for i in range(5): if abs((p-2+i)%Largeur-p%Largeur)<=2 : s=s+Ker[10+i]*Pix[p-2+i] else: continue for i in range(5): if p+Largeur<Largeur*Hauteur: if abs((p+Largeur-2+i)%Largeur-(p+Largeur)%Largeur)<=2 : s=s+Ker[15+i]*Pix[p+Largeur-2+i] else: continue else: break for i in range(5): if p+2*Largeur<Largeur*Hauteur: if abs((p+2*Largeur-2+i)%Largeur-(p+2*Largeur)%Largeur)<=2 : s=s+Ker[20+i]*Pix[p+2*Largeur-2+i] else: continue else: break newPix.append(s) return newPix #============================================================ # Définition du noyau noyau=[0,0,0,0,0, 0,0,1,0,0, 0,1,-4,1,0, 0,0,1,0,0, 0,0,0,0,0] # L'image a 3 composantes :RGB im = Image.open("rose.jpg") w,h=im.size #Séparation des composantes => tuple de 3 images ImagePixelsRouges,ImagePixelsVerts,ImagePixelsBleus=im.split() #transformation de l'image en liste de pixels ListePixelsRouges=list(ImagePixelsRouges.getdata()) ListePixelsVerts=list(ImagePixelsVerts.getdata()) ListePixelsBleus=list(ImagePixelsBleus.getdata()) ListePixelsRouges=produit_convo(ListePixelsRouges,noyau,w,h) ListePixelsVerts=produit_convo(ListePixelsVerts,noyau,w,h) ListePixelsBleus=produit_convo(ListePixelsBleus,noyau,w,h) ImagePixelsRouges.putdata(ListePixelsRouges) ImagePixelsVerts.putdata(ListePixelsVerts) ImagePixelsBleus.putdata(ListePixelsBleus) imgnew = Image.merge('RGB',(ImagePixelsRouges,ImagePixelsVerts,ImagePixelsBleus)) imgnew.save("Convolution.jpg") im.close() imgnew.close() |