Les objets fractals sont des structures invariantes par changement d’échelle. Nous allons commencé par voir celles portant le nom de Waclaw Sierpinski (1882-1969).
Le triangle de Sierpinski
On part d’un triangle équilatéral coloré. En joignant les milieux des côtés, on obtient un triangle équilatéral central que l’on met en blanc et des triangles équilatéraux colorés. On répète l’opération pour les triangles colorés. On réitère le procédé un nombre n arbitraire de fois.

Le tracé de cette figure s’appuie sur une fonction récursive (c’est à dire qui s’appelle elle-même). L’idée est de dire qu’un triangle de Sierpinski au rang n n’est autre que la réunion de trois triangles de Sierpinski au rang n−1. Les coordonnées des sommets des triangles sont bien-sûr différentes, il faudra donc mettre en données les coordonnées des sommets du triangle « père », puis déterminer les coordonnées des sommets des triangles « fils ».
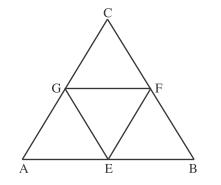
Plus précisément, l’algorithme va partager un triangle « père » ABC dont les sommets ont pour coordonnées A(xA,yA), B(xB,yB), C(xC,yC), en quatre triangles : trois triangles « fils » AEG, EBF, GFC et un triangle central EFG où E désigne le milieu de [AB], F le milieu de [BC] et G le milieu de [AC]. Puis il recommence l’opération pour tous les triangles « fils ».
Exercice 1 :
La fonction récursive est donc :
 |  |
Appliquez cet algorithme à la main en complétant la figure ci-dessus que vous aurez préalablement reproduite sur votre cahier.
Enfin tester l’algorithme suivant utilisant le module Pygame :
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
import numpy as np import pygame from pygame.locals import * pygame.init() black = (0, 0, 0) white = (255, 255, 255) blue = (0, 0, 255) green = (0, 255, 0) red = (255, 0, 0) size = [640,640] fenetre = pygame.display.set_mode(size) fenetre.fill(white) def PointMilieu(Pt1,Pt2): return [(Pt1[0]+Pt2[0])/2 , (Pt1[1]+Pt2[1])/2] def triangle(A,B,C,n): if(n>0): pygame.draw.polygon(fenetre,black,[A,B,C],1) triangle(A,PointMilieu(A,B),PointMilieu(A,C),n-1) triangle(PointMilieu(A,B),B,PointMilieu(B,C),n-1) triangle(PointMilieu(A,C),PointMilieu(B,C),C,n-1) Pt1=[10,630] Pt2=[630,630] Pt3=[320,93] triangle(Pt1,Pt2,Pt3,8) pygame.display.flip() continuer=True while continuer: for event in pygame.event.get(): if event.type==QUIT: pygame.quit() continuer=False |
Le Tapis de Sierpinski :
 |  |
Le tapis se fabrique en découpant le carré « père » en neuf carrés égaux selon une grille de trois par trois, et en supprimant la pièce centrale, puis en appliquant cette procédure aux huit carrés restants un nombre n de fois.
Exercice 2 :
Ecrivez la fonction carre du code suivant pour obtenir un tapis de Sierpinski :
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
import numpy as np import pygame from pygame.locals import * pygame.init() black = (0, 0, 0) white = (255, 255, 255) blue = (0, 0, 255) green = (0, 255, 0) red = (255, 0, 0) size = [730,730] fenetre = pygame.display.set_mode(size) fenetre.fill(white) def carre(x,y,cote,n): if(n>0): cote=int(cote/3) # pygame.draw.rect(screen,color,[x,y,width,height],line_thickness) # Le rectangle est rempli si le dernier paramètre est absent pygame.draw.rect(fenetre,black,[x+cote,y+cote,cote,cote]) # # # # # # # # carre(0,0,729,6) pygame.display.flip() continuer=True while continuer: for event in pygame.event.get(): if event.type==QUIT: pygame.quit() continuer=False |

