2 – Ensemble de Mandelbrot

En mathématiques, l’ensemble de Mandelbrot est une fractale définie comme l’ensemble des points c du plan complexe pour lesquels la suite de nombres complexes définie par récurrence par : $\begin{cases} z_0=0\\ z_{n+1}=z_n^2+c \end{cases}$ est bornée.

Prenons le plan des nombres complexes (que l’on peu assimilé au plan à deux dimensions x et y), chaque point du plan est représenté par un nombre complexe différent c.

Pour chaque point du plan :

On considère la suite de nombres complexes (z_n) définie par la relation de récurrence ci-dessus où c est l’affixe associé au point du plan choisi
Si cette suite diverge (ce qui est le cas dès que son module Ι z_nΙ dépasse 2) on colorie le point en blanc (ou en couleur en fonction du nombre du nombre d’itération nécessaire pour que le module dépasse 2). Dans le cas contraire, après un certains nombre d’itérations on considère la suite bornée et on colorie le point en noir.

On répète ce processus pour chaque point du système de coordonnées. L’ensemble des points noir est l’ensemble de Mandelbrot.

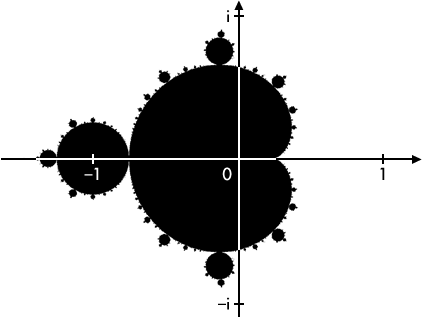
Exercice 1 :

Editez et exécutez le script suivant qui fait apparaître l’ensemble de Mandelbrot.

from PIL import Image

# Bornes de C
CoinSupGau    = complex(-2,1.1)         # limite -2.1+1.2i
CoinInfDroit  = complex(0.6,-1)         # limite 0.6-1.2i         

NbIterations = 128

#Definition de l'image
L = 512
H = int((-CoinSupGau.imag+CoinInfDroit.imag)*L/(CoinSupGau.real-CoinInfDroit.real))
image = Image.new("RGB", (L, H))

#Coefficient de mise à l'échelle
bx =CoinSupGau.real
ax = (CoinInfDroit.real - CoinSupGau.real)/(L-1)
by=CoinSupGau.imag
ay= (CoinInfDroit.imag-CoinSupGau.imag)/(H-1)

for y in range(H):
     cy=  ay*y+by
     for x in range(L):
        cx=  ax*x+bx
        c = complex(cx, cy)
        z=0
        for Iteration in range(NbIterations):
            if abs(z) > 2.0: break 
            z = z **2 + c
        red= int(Iteration% 4 * 64)               #256 niveaux
        green = int( Iteration % 8 * 32)
        blue= int( Iteration % 16 * 16)
        image.putpixel((x, y), (red,green,blue))

image.show()

from PIL import Image

# Bornes de C

CoinSupGau = complex(-2,1.1) # limite -2.1+1.2i

CoinInfDroit = complex(0.6,-1) # limite 0.6-1.2i

NbIterations = 128

#Definition de l'image

L = 512

H = int((-CoinSupGau.imag+CoinInfDroit.imag)*L/(CoinSupGau.real-CoinInfDroit.real))

image = Image.new("RGB", (L, H))

#Coefficient de mise à l'échelle

bx =CoinSupGau.real

ax = (CoinInfDroit.real - CoinSupGau.real)/(L-1)

by=CoinSupGau.imag

ay= (CoinInfDroit.imag-CoinSupGau.imag)/(H-1)

for y in range(H):

cy= ay*y+by

for x in range(L):

cx= ax*x+bx

c = complex(cx, cy)

z=0

for Iteration in range(NbIterations):

if abs(z) > 2.0: break

z = z **2 + c

red= int(Iteration% 4 * 64) #256 niveaux

green = int( Iteration % 8 * 32)

blue= int( Iteration % 16 * 16)

image.putpixel((x, y), (red,green,blue))

image.show()

Modifiez ensuite le programme pour que la zone affichée soit limitée par les coins de coordonnées (-0.2 ; 1.1) et (-0.1 ; 1.0).

Exercice 2 :

Proposez une interface graphique qui permet à l’utilisateur de :

choisir la zone à afficher (filtrer la saisie pour rester dans les limites de l’image)
choisir la largeur de l’image
interrompre le programme
être renseigné sur le temps d’attente via une barre de progression et l’affichage du temps restant

Mathinfo

Activités, ressources, informations relatives aux cours de mathématiques ou d'informatique

2 – Ensemble de Mandelbrot