Un arbre est fractal en ce sens que ses branches maîtresses, issues du tronc, sont chacune des arbres en réduction.
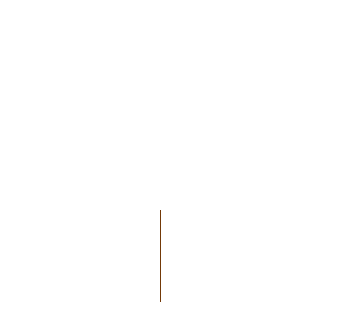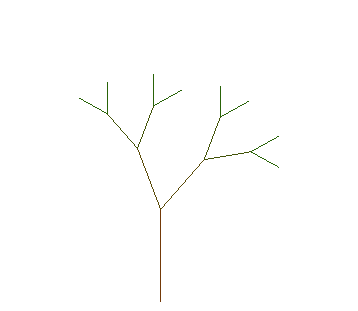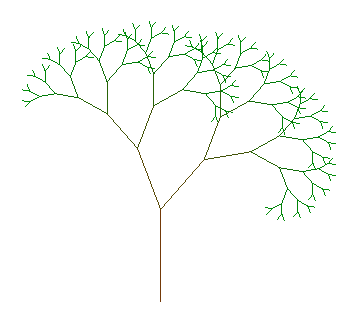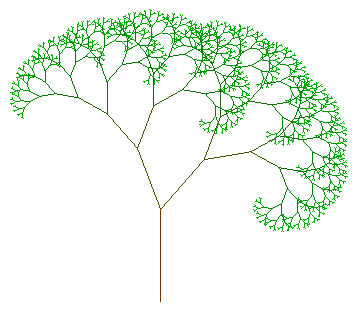
Le tracé de cet arbre se fait de manière récursive :
Il commence par le dessin d’un segment qui est défini par son point de départ, sa longueur et son angle ( orientation ). Tant que la profondeur n’est pas atteinte, à chaque extrémité de segment démarrent deux nouveaux segments.
Exercice 1 :
Editer le code suivant et compléter les fonctions « segment » et « arbre » afin d’obtenir un arbre fractal.
Les variables utilisées correspondent aux coordonnées de début et de fin du segment, à sa longueur et à l’angle qu’il fait avec l’horizontale selon le schéma suivant :
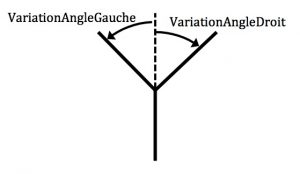 | 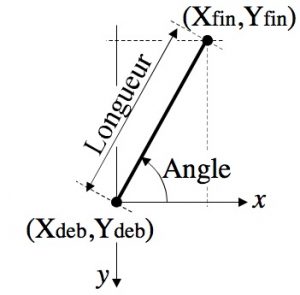 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
import pygame from math import * pygame.init() window = pygame.display.set_mode((600, 600)) pygame.display.set_caption("Fractal Tree") screen = pygame.display.get_surface() K= 10 VariationAngleDroit=15 VariationAngleGauche=-15 def segment(Xdeb, Ydeb, Angle, Longueur): "Trace le segment et renvoie les coordonnées du point extème." Xfin = # à compléter Yfin = # à compléter pygame.draw.line(screen, (255,255,255), (Xdeb,Ydeb), (Xfin, Yfin), 2) return # à compléter def arbre(Xinit, Yinit, Angle, Profondeur): if Profondeur>0: Longueur = Profondeur*K Xterm,Yterm = segment(Xinit, Yinit, Angle, Longueur) arbre(# à compléter) arbre(# à compléter) def input(event): if event.type == pygame.QUIT: exit(0) arbre(300, 550, 90, 9) pygame.display.flip() while True: input(pygame.event.wait()) |
Exercice 2 :
Modifiez le programme pour que l’arbre se penche, comme s’il était exposé au vent.
Exercice 3 :
Modifier le programme en utilisant la fonction ‘randrange’ du module ‘random’ pour introduire des aléas :
a) dans les longueurs des segments
b) dans les angles.
Pour plus de réalisme on souhaite donner de l’épaisseur au tronc. La figure ci dessous shématise la branche d’un arbre qui se subdivise en deux branches, chacune d’elle pouvant se subdiviser à son tour en deux branches etc..
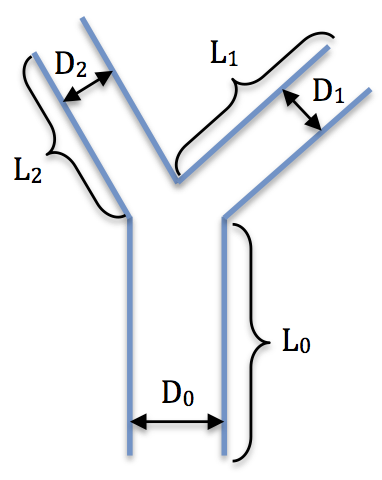
Les scientifiques ont beaucoup discuté sur cette représentation mathématique des arbres, le premier étant Léonard de Vinci. Il a écrit que le diamètre de la branche initiale est égal à la somme des diamètres des 2 branches suivantes, ces diamètres étant affectés d’un exposant alpha α, appelé exposant du diamètre (relation (1)).
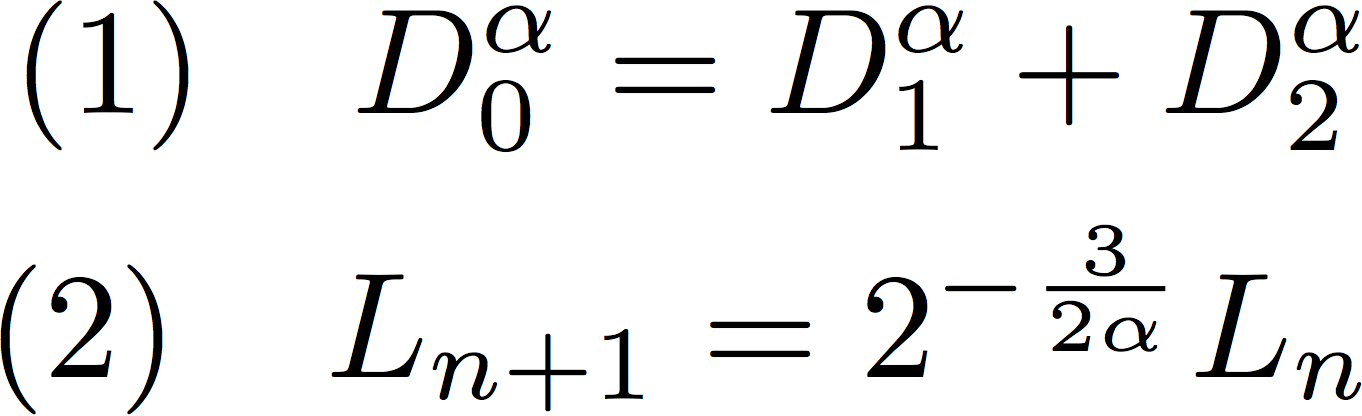
On admet que pour les arbres botaniques, alpha est égal à 2, alors que pour l’arbre bronchique (les poumons se représentent aussi par un arbre fractal), alpha doit être égal à 3, et pour le système artériel alpha doit être égal à 2,7. L’équation (2) donne la relation entre les longueurs de deux branches successives.
Selon le choix de alpha, de la longueur initiale L, du diamètre initial D et de l’angle fait par les 2 branches, l’aspect de l’arbre obtenu est très différent.
Si pour simplifier on considère les diamètres des branches filles identiques, la relation (1) permet d’exprimer la relation entre deux branches successives par :
![]()
Exercice 4 :
Modifier votre programme pour tenir compte des épaisseurs et longueurs des troncs selon la règle ci-dessus.
Le dernier paramètre de l’instruction pygame.draw.line correspond à l’épaisseur du trait.
