L’attribut transform permet d’effectuer :
- des translations
- des rotations
- des mises à l’échelle (en gros, des zooms)
Il faut bien que vous compreniez que ces transformations agissent sur le système de coordonnées.
Commençons par la Rotation qui permet de « tourner » le système de coordonnées d’un certain angle.
| Au départ nous avons : | après une rotation, nous obtenons ceci : |
|---|---|
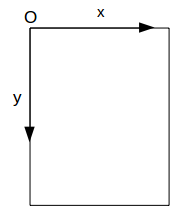 | 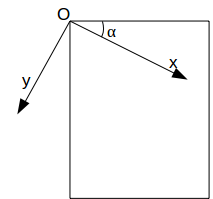 |
Pour effectuer une rotation d’un angle α, il suffit d’utiliser l’attribut transform en rajoutant transform = ″rotate(α)″
| sans le transform="rotate(α)" | avec le transform="rotate(α)" |
|---|---|
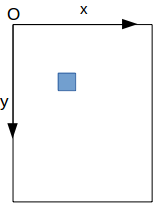 | 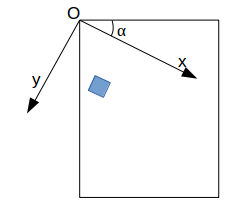 |
À faire vous-même 4.1
Saisissez et testez ce code
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
<!doctype html> <html lang="fr"> <head> <meta charset="utf-8"> <title>Dessiner avec svg</title> <link rel="stylesheet" href="style.css"> </head> <body> <svg id="dessin"> <rect x="50" y="60" width="20" height="20" transform="rotate(30)"/> </svg> </body> </html> |
À faire vous-même 4.2
Saisissez et testez ce code
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
<!doctype html> <html lang="fr"> <head> <meta charset="utf-8"> <title>Dessiner avec svg</title> <link rel="stylesheet" href="style.css"> </head> <body> <svg id="dessin"> <rect x="100" y="100" width="20" height="20"/> <rect x="100" y="100" width="20" height="20" transform="rotate(30)"/> </svg> </body> </html> |
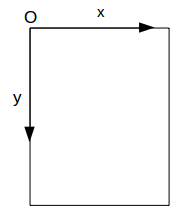
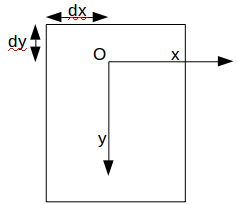
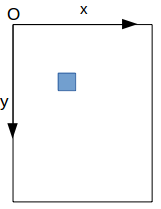
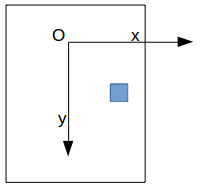
« translate » permet de faire faire une Translation au système de coordonnées :
pour cela il faut utiliser l’attribut transform = ″translate(dx,dy)″
| avant | après on obtient ceci |
|---|---|
 |  |
 |  |
À faire vous-même 4.3
Saisissez et testez ce code
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
<!doctype html> <html lang="fr"> <head> <meta charset="utf-8"> <title>Dessiner avec svg</title> <link rel="stylesheet" href="style.css"> </head> <body> <svg id="dessin"> <rect x="100" y="100" width="20" height="20"/> <rect x="100" y="100" width="20" height="20" transform="translate(250,150)"/> </svg> </body> </html> |
« scale » ne devrait pas vous poser de difficultés :
Attention, comme pour rotate ou translate, c’est le système de coordonnées qui se trouve affecté par l’application de scale. Scale permet donc de modifier les échelles : dilatation de l’échelle si l’argument est supérieur à 1, contraction de l’échelle si l’argument est compris entre 0 et 1.
À faire vous-même 4.4
Saisissez et testez ce code
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
<!doctype html> <html lang="fr"> <head> <meta charset="utf-8"> <title>Dessiner avec svg</title> <link rel="stylesheet" href="style.css"> </head> <body> <svg id="dessin"> <rect x="100" y="100" width="20" height="20"/> <rect x="300" y="100" width="20" height="20" transform="scale(3,3)"/> </svg> </body> </html> |
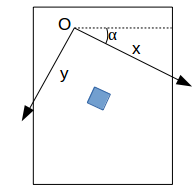
Il est possible de combiner « rotate », « translate » et « scale »:
attention l’ordre d’application à son importance
À faire vous-même 4.5
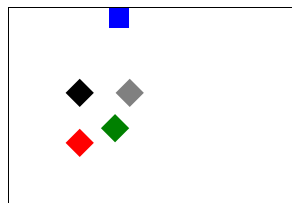
Complétez le code suivant avec les couleurs (fill) correctes pour obtenir cette figure :
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
<!doctype html> <html lang="fr"> <head> <meta charset="utf-8"> <title>Dessiner avec svg</title> <link rel="stylesheet" href="style.css"> </head> <body> <svg id="dessin"> <rect x="100" y="0" width="20" height="20" fill="????" stroke="none"/> <rect x="100" y="0" width="20" height="20" fill="????" stroke="none" transform="rotate(45)"/> <rect x="100" y="0" width="20" height="20" fill="????" stroke="none" transform="translate (0,50) rotate(45)"/> <rect x="100" y="0" width="20" height="20" fill="????" stroke="none" transform="translate (50,0) rotate(45)"/> <rect x="100" y="0" width="20" height="20" fill="????" stroke="none" transform="rotate(45) translate (50,0)/> </svg> </body> </html> |
Il est possible, à l’aide de la balise <g> de regrouper vos dessins afin de leur faire subir des transformations (rotation, translation ou changement d’échelle) de façon simultanée.
À faire vous-même 4.6
Saisissez et testez ce code
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
<!doctype html> <html lang="fr"> <head> <meta charset="utf-8"> <title>Dessiner avec svg</title> <link rel="stylesheet" href="style.css"> </head> <body> <svg id="dessin"> <g transform="rotate(45)"> <rect x="100" y="0" width="20" height="20"/> <circle cx="140" cy="10" r="20" fill="red"/> </g> </svg> </body> </html> |
Il suffit d’appliquer la transformation au groupe défini avec la balise <g> pour que le dessin dans son ensemble subisse la transformation.
À faire vous-même 4.7
En repartant de l’exemple que vous avez développé dans le « À faire vous même 3.5 », essayez de reproduire (à peu près) ce dessin :

